人にわかりやすく物事を伝える
はじめに
生きていると物事を伝えることが求められることがあります。それは論文であったり、ブログであったり、はたまた面接であったり様々な形で求められます。そこで多くの人がこのようなレビューを受けるのではないでしょうか
「わかりにくい。素人でもわかりやすいようにしてほしい」
一方であなたは心の奥底でこう思うかもしれません(あるいは言ってしまうかも。)
(この話を聞くための前提知識を知らない人に教えることは無理)
このような要求を飲もうとすればするほど資料が長くなり、今度は 「長いから聞きたくない」 と言われるようになり、しかし初心者向けにしすぎると既存資料と同じ内容になってしまったり、厳密性を損なってしまうことも多々あります。
一般に、「短時間で誰でも分かる説明」と「内容の難しさ」はトレードオフの関係にあり、どちらかを取ればどちらかを犠牲になります。そのような中で
「内容はそのままでわかるようにしてほしい」
という要求は無理があるのです。自分も YouTubeをやっていて ありがたいことに多くの人に見てもらっている以上、「内容が難しい」という声を聞くことは少なくありません。
様々な場面で求められる「わかりやすい説明」に対してどうアプローチすればよいのか、自分なりの考えがあるので今日はそれを記載します。
物事を伝える上での3要素
自分は物事を伝える上で、以下の3要素を常に考えています。
- なぜ自分はそれを伝えるのか
- 聞く対象は誰か
- 対象は聞いた後どのような状態になって欲しいのか
重要なのは聞き手目線になることで、「話し手が伝えたいから」 という観点は基本的にノイズになります。例えば、「ここで苦労したから感情をシェアしたい」 という欲求はよくあると思うのですが、聞き手の気持ちになって 「聞き手はこういう要素に興味があるだろうから話そう」 であったり、 「聞き手にこういう要素があるのでこの検証は再現が難しく新規性があることを伝えよう」 であったり、伝えたいことを聞き手目線に変換して上げることが重要です。
また聞き手目線の気持ちになりすぎて、伝える目的を忘れてはなりません。物事を伝えるという労力をかけているのですから、「その対価として何を得たいのか」は忘れないようにしましょう。
(例えば専門家にレビューしてもらって正当性を判断する、であったり専門外の人の意見を聞いて新たな観点を得るだったり、面接に合格するだったり。)
「わかりにくい」と言われたときに犠牲にするもの
ここで「わかりにくい」と言われたとき、伝える技量には限りがあるので、何かを犠牲にする必要があります。大きく分けて2つの戦略を取っています。
- 聞く対象を限定する: 「わかりにくい」といった人を対象外とする
- 聞いた後の状態のハードルを下げる
聞く対象を限定する際は、「それが適切か」を検討する必要があります。発表中に聞く人が一人も理解できなければ発表する意味もないですし、面接等で専門外の人に説明するときに高度な前提知識を要求してもしかたがありません。
ただし聞く対象が多ければ多いほうがいいのは間違いないので、「あなたは前提知識がない」と突っぱ過ぎないようにも気をつけましょう。
ハードルを下げる方向に関しては、例えば物事を伝える上での「結果だけ」を伝えることで簡単に「結果」は伝えることはできますよね。よくニュースやX(旧Twitter)で見る「どこそこ大学の研究室がこういうことができた(具体的な内容には言及しないし多くの人はみない)」といった形式は、多くの人にもわかってもらえます。
しかし残念ながらあなたの設定した「対象」は結果だけを求めている場合もあれば、それの何が嬉しいかを求めている場合もあれば、その証明を求めている場合もあります。
これらを両立して満足させるために、「動的に内容を難しくする」という手段があります。
最初は誰でもわかるように→途中からは段々と難しくしていく
といったように。発表等であれば「これを聞きたい人はここまで聞いてほしい。ここからは分からなくて問題ない」というラインが 聞き手にとっても わかりやすいと良いですね。こうすることで「聞き手の求めていることに対するわかりやすさ」と「説明する難易度」をある程度両立できることが多い気がします。「全部わからなくていいんだよ。」というのをうまく伝えられるといいですね。
あなたが「わかりにくい」と言うときは
あなたがレビューをする立場の場合、「わかりにいからわかりやすくしてほしい」というコミュニケーションは 聞き手視点 にとって大変つらい要求であることがわかったかと思います。また伝わる伝わらないは0,1のバイナリーではなく、40%くらいは伝わっているのような状態もありえます。
では 聞き手の気持ちになって 「わかりにくい」 を伝えるためにどうすればよいでしょうか。
聞く対象者の認識を合わせる
レビュワーと執筆者で聞く対象の認識のズレはよくあります。「この資料を聞く上で必要な前提知識は何になりますか?」「この資料は誰が聞く想定ですか?」とまずはどのような人が聞くのかの認識を合わせましょう。
執筆者の「伝える意図」や「聞き手の最終的な状態」の認識を合わせる
ここもよくズレます。執筆者は「正しさ証明したいので厳密な証明や手順を紹介したい」と思っているのに対し、レビュワーは「成果をアピールしたいので結果を伝えられれば十分だ」と感じていれば不毛なレビューになると思います。特にレビュワーの立場が上であれば、執筆者は機械的にその通りに修正してしまうこともよくあるので、全員が資料に対して納得できる前提のすり合わせをしましょう。
どこがわかりにくいか言語化する
「わかりにくい」とは様々な要素に起因して発生します。自分がよくする指摘は以下のとおりです。
- 何を伝えたいのかわからなかった / 何を意図しているのかわからなかった
- 必要な前提知識を説明していないので内容が理解できなかった
- 日本語がおかしい(主語が存在しない、主述関係がおかしい、接続詞がおかしい)ので主張が理解できなかった
- 内容が正しくない
- 事実か仮説かわからない
- タイトルと内容が一致していない(そのスライドの伝えたいと思われる内容が理解できなかった)
特に最初2つに関しては自分では気づきにくい要素で客観的意見が必要になります。みんな知ってると思ってたけど実はマイナーだった。なんてことはよくありますよね。
また知らず知らずのうちに、感情的に自分が面白いと思い物事を伝えてしまうこともよくあります。対象とする聞き手がそれを楽しいと思ってくれるならいいのですが、そうでないのでただただ自分の好きなことを喋るだけのアレな人になってしまいますね。
あなたが「わかりにくい」と言われたときは
あなたが「わかりにくい」と言われたときは、逆に↑の内容をレビュワーとすり合わせましょう。
人にわかりやすく物事を伝える
聞き手を絞ったり、ハードルを下げたりするのは仕方がない場合であり、同じ聞き手、同じ内容、同じ時間で伝えられると良いことに間違いはありません。
厳密な証明や形式的な内容に関しては避けにくいかもしれませんが、提案手法のメリットなどは多くの人に伝えられるべきであり、また正しい日本語や正しい図を用いることでそれを広げられる可能性があります。
どうしても自分の感情が邪魔してしまい、「聞き手の気持ちになる」ことは人間にとって難しいことで、一朝一夕にできるようなことではありません。
発表や面接、論文だけではなく、日頃の友達とのコミュニケーションなどでも「物事を伝える機会」は多く訪れます。
「自分が楽しい」だけではなく、「聞き手が楽しい」と思える時間を作れるように努力することでこういった能力が身につくのではないかと考えています。お互いに取ってお互いが楽しいと思える関係性を作れるといいかもしれませんね。
またこういったスキルの積み重ねが、多くの人や企業が評価する「コミュニケーション能力」というやつなのかもしれません。
半年チャンネル登録者数が100人だった無名VTuberがチャンネル登録者数3400人になるまでやったこと、これからやること
この記事で伝えたいこと
YouTubeをやっていると、どうしても「チャンネル登録者数を増やしたい!」という気持ちになる人は多いと思います。 自分は2019年10月くらいにVTuberとしてデビューしました。当時は全くの無名で、半年ほどチャンネル登録者数は100人以下でしたが、コツコツ活動を積み重ねて今では3400人ほどになりました。(https://www.youtube.com/c/kurenaif)今でも変わらずチャンネル登録者数を増やし続けています。
この記事では数年間YouTube活動をしていく上で、自分が「やってよかったな」とか、「これはこういうことだったんだな」とか思うことがいくつかあったのでまとめて行きたいと思います。
この記事をきっかけになにか自身の知名度を上げることができるきっかけになってくれたら嬉しいです。
まず前提として、チャンネル登録者数を増やすのは難しい。
あなたは普段よくチャンネル登録をしますか?自分はしません。 自分がチャンネル登録をするときは以下のとおりです
- 始めたてのチャンネルで、とても良い動画だった。チャンネル登録をして応援して、続きの動画を出すモチベーションになってほしい。
- 動画で特定のキーワードで調べると、高頻度で新しい動画が出てくる。それを毎回見てしまう。ある日その人が好きなんだなということに気づいて、ふとチャンネル登録をする。
- チャンネル登録者数を増やすことを目標にしている。頑張っているし、好きなのでチャンネル登録をして応援したい。
といったように自分の感性で考えてみると、チャンネル登録者数を増やすのは難しいよなって思います。というのも、YouTubeのリコメンドシステムが優秀なので、チャンネル登録をしなくても十分楽しめるんですよね。YouTubeのリコメンドを超える何かがないとチャンネル登録はしないんだろうなって思います。
あなたはどういったときにチャンネル登録をしますか?あなた自身がチャンネル登録をしたいと思うチャンネルにすることが最も大切だと思います。
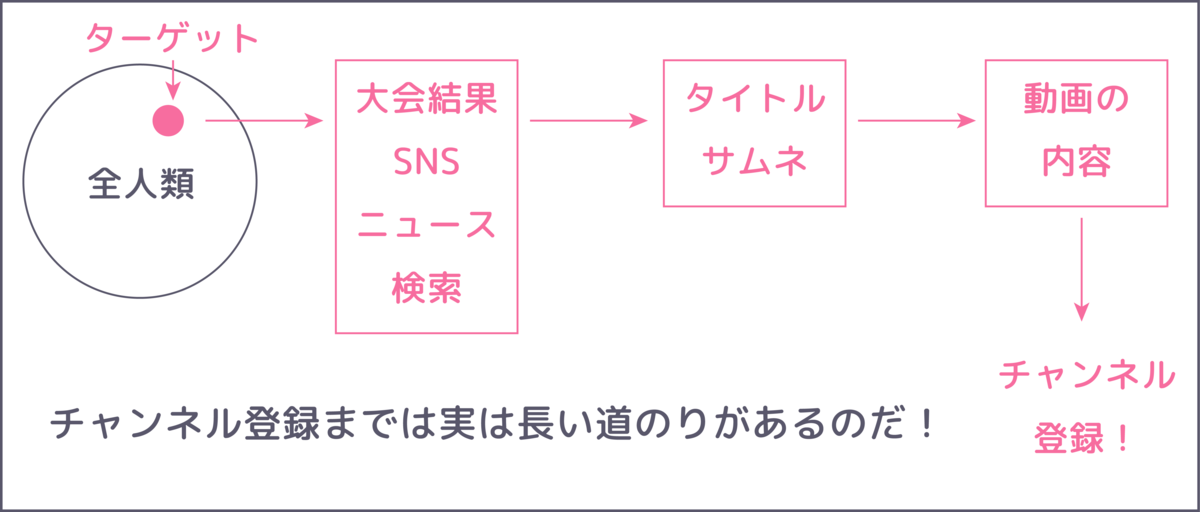
ターゲット層を決める
視聴者に「チャンネル登録をしたい!」という気持ちにさせたあとは、ターゲット層を定めることが重要です。 しっかりと焦点を絞ることで、視聴者層が想像しやすくなり、より解像度高く視聴者目線になることができます。
年齢層を絞ることで話題も変わります。ゲームを題材にする場合は、どの程度ゲームに前提知識を要求するか?でも変わってきます。ターゲット層を絞れば絞るほど、視聴者に満足してもらいやすいコンテンツを作りやすくなると思います。また、「きちんと狙った視聴者層が満足したか?」という振り返りもできるので、改善にもつなげることができます。
自分の場合はベースとして以下をターゲット層にしています。
- 基本的なプログラミングはできる。いろんなプログラミング言語はあるけど大まかには読める
- 高校数学相当の知識はある。数学に苦手意識がない
- ハッキングの原理を知りたい。攻撃することそのものにはあまり興味はない
また、各動画には更に細かく対象者をきめていますし、動画ごとの離脱時間を考慮して時間ごとに対象者をより細かく区切っています(後半になるほど専門的になるように設計しています)。
あなたが作ろうとしているチャンネル、1動画、1配信は誰に向けて作っていますか?その人達が満足できる内容を提供できていますか?
ターゲット層がクリックするタイトルやサムネを作る
狙った層に向けて動画を作るぞ!と考えても、動画にリーチすらしなければ意味がありません。ここで「あなたはどういう動画であればクリックしますか?」ということを考えます。
よく、「見やすいサムネが重要」とか、「こういうタイトルを付けるといい!」みたいな話が上がりますが、そういう話が多すぎてよくわかりませんw(実際サムネなどは工夫していますが効果があるのかはよくわかりませんw)
自分はそういうテクニックはあくまでも表現したい内容をうまく伝える技術であって、結局は内容が大事なんじゃないかなと思います。自分は、以下のようなものを見たときにクリックをします。
- 自分がしならさそうな内容がそこにある、動画を見ると学びになりそう
- タイトルからしてすごいことが保証されている、内容が気になる…(世界1位やTASなど)
- 動画が毎回面白いのでチャンネルをアイコンを見ただけでクリックしてしまう
- 動画のサムネを見て、「確かにこれなんでだろうな…」みたいな気持ちになる
- サムネを見て、「どうしてこうなったんだ…」と仮定が気になる
あなたが作った動画はあなたがクリックしてみようと思いますか?あなたが決めたターゲット層はどうでしょうか?
ターゲット層の流入経路を知る
さて、タイトルとサムネもできた、クリックもしてもらえそうだ!と思ったとしても、残念ながらターゲット層のYouTube上に表示されなければ、クリックする機会も得られません。ここで、「SNS」や「検索キーワード」という言葉が出てきます。そして、あなた自身が「どうやってその界隈のことを知ったのか?」というきっかけを考えることも大事です。
効果があるかはわかりませんが、以下は自分が気をつけていることです
- できる限り同じようなタイトルは付けない。いろんなキーワードで検索したときに、自分の動画のどれかはヒットするようにする。
- 特定の流入が見込める単語において、検索上位に位置づけるように頑張る(高評価率や再生数など)
- TwitterではしつこいぐらいにRTする(意外と何度もRTしても認知してもらえないことが多いです)
- 定期的に大会などで成績を残す
特に大会で好成績を残すことは認知してもらいやすくなるので、確実な手段かなと思います。
流入を増やそうとして、煽るようなタイトルをつけることはおすすめしません。 あなたはそのタイトルをみて動画を閲覧し、チャンネル登録をしようと思いますか?煽るようなタイトルでチャンネル登録をするような人のコミュニティの運営者としてやっていく覚悟はありますか? 一度落とした信頼はなかなか回復しないので、適切なタイトルを付けることをおすすめします。(でも多少の誇張はいいと思います)
再生数は全てではない
たくさん再生されていたとしても、意外とチャンネル登録者数は増えません。傾向として、技術系は再生数に対して多く、ゲームは再生されてもなかなかチャンネル登録してもらえない印象です。
また再生数はタイトルやサムネイルだけではなく、その界隈の大きさや言語や時差など、あなたではどうしようもないものに依存している可能性があります。数撃ちゃ当たる、といえばそうなのですが、個人的にはまずあなたの動画を見てくれる人を大切にし、その人達に対してチャンネル登録をしたい!と思わせることが重要ではないかと思います。 そうやって基盤を作った後、再生数を伸ばすことで爆発的にチャンネル登録者数を増やせるのではないかと思います。
少なくともボクは1万再生の動画は持っていません。
動画内でチャンネル登録を訴求する
多くのYouTubeチャンネルで「チャンネル登録してね!」という言葉をよく耳にすると思います。実際これはかなり効果があり、チャンネル登録者数増加につながっています。
自分は動画を見ているとき、「チャンネル登録をするかどうか」という選択肢はありません。単純に認識の外です。チャンネル登録をしてね!と言われて初めてチャンネル登録をするかどうか考えます。
おそらくですが、多くの人は動画を見ているとき、チャンネル登録をするかどうかの天秤にすらかけておらず、「不戦敗」のような形になっているのではないかと思います。せめて「チャンネル登録お願いします!」と言及し、天秤には載せてあげましょう。その上で負けたなら仕方なしです。
また、チャンネル登録者数を祝うことも重要です。あなたがやった行いに対して、リアクションがあると嬉しくなりますからね。その点でもチャンネル登録者数記念はとてもいいと思います。
以上がまずは基盤を作る部分です。基盤を作った後は拡張を行います。
ターゲット層の「クラスタ」を意識し、別クラスタに訴求する
クラスタとは、似たような属性や共通点を持つ集団だと自分は考えています。ターゲット層を決め、その層を満足するような動画を出し続けているといずれ限界が訪れます。そうなったときにターゲット層を考え直すことです。
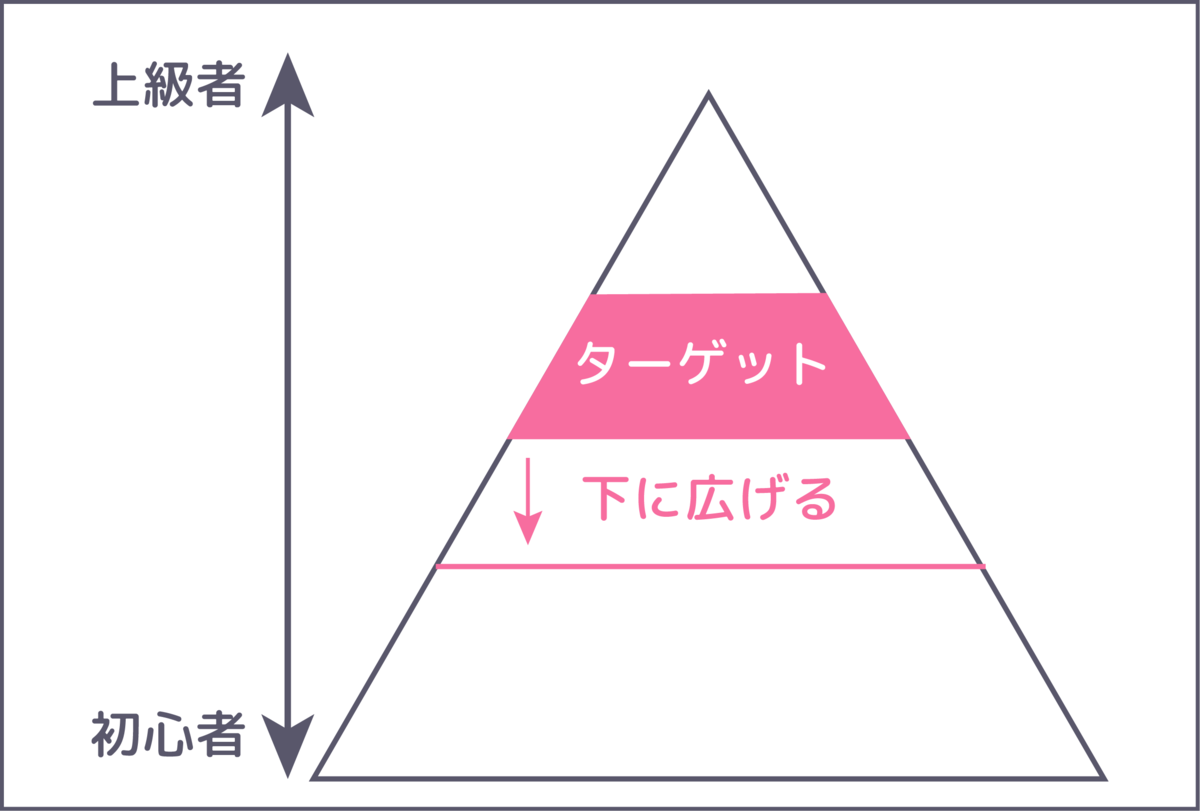
初心者向けの内容の充実
まず簡単な方法としては、より初心者向けに訴求する方法です。初心者向けの内容は大抵の場合レッドオーシャンですし、内容も似たりよったりになってしまいがちになってつまらくなってしまいます。何も武器がない状態で挑むと砂漠の中の一粒の砂のような存在になってしまいますが、きちんとターゲット層を決め、しっかり基盤を整えたあとであれば話は別です。その頃には、「あなた」という付加価値が生まれているでしょうし、支えてくれるリスナーもいるでしょう。少しずつ初心者向けの内容を充実させていき、コミュニティを大きくしていきましょう。
自分の場合は、実際に初心者に入門をしてもらう動画を作ったりして訴求しています。 youtu.be
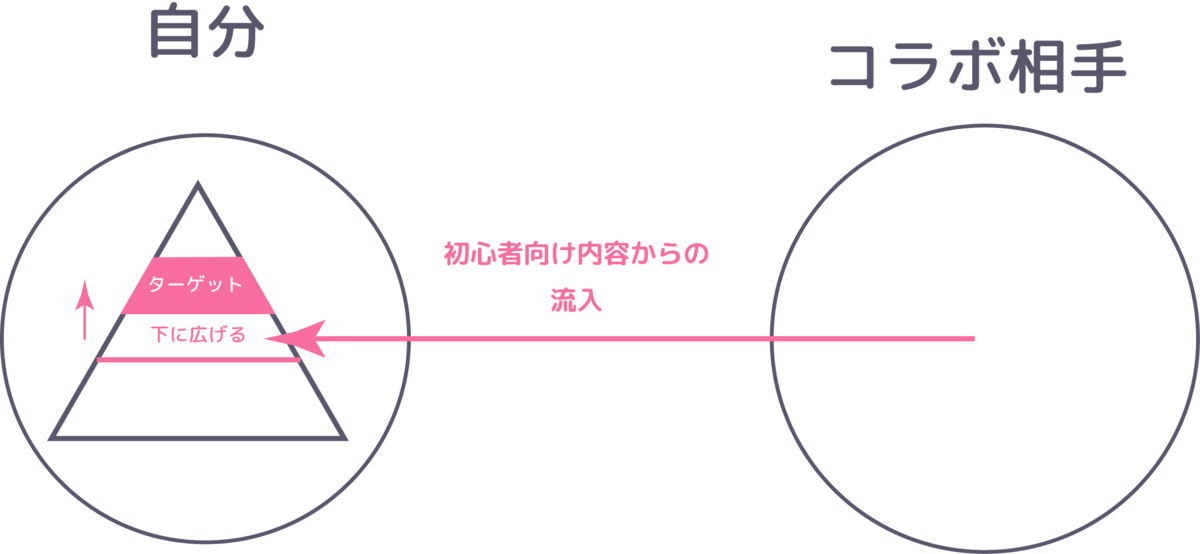
コラボ
コラボは自分のことを知ってもらうとてもよい機会です。お互いのYouTuber同士が作った基盤を連結させる機会になります。
全く興味がない人たちに、少しでも興味を持ってもらうきっかけになります。積極的にやっていきましょう!
ここで、初心者向けの内容があると流入してもらえやすくなるので、「まずはこれを見るといいよ!」と言った動画を作っておきましょう。(これをするための「初心者向けの内容の充実」でした。)
新しいことを初めてみる
ゲーム実況を分析していると、ある一つのゲームで有名になった人が新しいゲームにも手を出した後、いろいろなゲームに着手するようになることをよく見てきました。一つのゲームだとチャンネル登録者数がある程度で止まっていた人が、それ以降よく伸びるようになったと感じます。
このように、新しいことを始めることで、別のクラスタに訴求できる可能性があります。その活動の中で、自分の普段の活動を紹介し、流入してもらう。と言った活動をすることでチャンネル登録者数を増やせるのではないか、と考えています。
ただ、そうするためには自分のことを好きになってもらい、自分の動画の初心者向け内容から更に自分のコアのターゲット層の動画に行き着いて貰う必要があります。遠い道のりですが、こういった道を整備することで「誰でも楽しめるコミュニティ」が形成できるのではないかと考えています。
kurenaifはどうしてきたの?そして今後の活動方針
今まではセキュリティの大会で結果を残し、その動画を作ることで特定のターゲット層にアプローチをしつつ、定期的に初心者向けの内容を作ったり、コラボをしたりすることでその層を広げていくことをしていました。
大会でも世界トップクラスの海外プレイヤーに認知もされており、上方向にはかなり良い感じだと思っています。一方で、最近は同じような活動をしていてもチャンネル登録者数の伸びが悪くなってきていることも感じています。セキュリティに興味がある層は大学等で定期的に排出されているのでじわじわ増えては行くと思いますが、これ以上の爆発的な増加は現在見込めません。
ここで2023年の活動方針の話になるのですが、2023年はゲーム実況などに手を出してみる、いろんなVTuber(技術系以外も!)とコラボをして、自分の存在を認知してもらう。視聴者との交流の機会を増やし、より視聴者のニーズの理解を深めていくことをしていきたいと思います。
この記事があなたのなにかの役に立てば嬉しいです!一緒に頑張りましょう!よかったらチャンネル登録してくださいね!↓↓↓
作問、動画作成の風景
はじめに
この記事は、CTF Advent Calendar 2022 の9日目の記事です。
8日目はbata24さんの「bata24/gefの機能紹介とか」でした。
すごい技術的な話の後にポエムみたいな話です。
この記事では普段kurenaifがどのようにして動画や問題を作っているのかを紹介します。
作問や教育コンテンツ作成の手助けになると嬉しいです
ネタ集め
ネタがなければ何も始まりません。まずはネタ集めをします。
とは言え、動画や問題を作りたい!と思ってからネタを集めるのではなく、普段から緩やかにネタを集め続けています。
例えば以下のようなものがネタになります。
身の回りにある「これってなんでこうなるんだろう?」「これをこう変えてみたら何がおきるんだろう?」というのが、特に動画や問題の原泉になることが多いですね。
SECCON2022の this_is_not_lsb は、「RSAのLSB Oracleは有名だけど、じゃあ逆にMSBはできないの?」と思ったことがきっかけでした。
その他具体的には以下のようなネタがありました。
- CORSではCSRFを守れそうな機能があるけど、実際どれくらい守れるの?
- AES-GCMはどうやって実装されているんだろう?
- 線形代数とRSAで面白いことできないかな?
- RSAのLSB Oracleが面白い!問題にしたい!
自分はアウトプットをしてまとめることが好きなので、こう思ったらだいたい動画や問題にしようと思うことができます。
ネタから問題原案へ
動画のようなアウトプットや教育に振り切ったコンテンツでは既存のアルゴリズムそのままを出せば良いのですが、SECCONのような競技の場では多少変形させたほうが良いです。「RSA LSB Oracleが面白かったからそのままだそう!」とはいかないのが難しいところですね。問題にするときはいくつか方法があります。自分がよく使う手段は以下です。
- 攻撃手法を組み合わせる
- 問題を簡単にする
- 問題を難しくする
- 問題を変形する
- 天啓を待つ
- めちゃめちゃ数式を変形して面白い形にならないか試す
「攻撃手法を組み合わせる」はとてもよく使われますね。例えば、SECCON 2022の「Wiches symmetric exam」では Padding Oracle AttackとAES-GCMの攻撃(名前知らん)の組み合わせですし、pqpqはGCDやらTonelli-Shanks algorithmやら色々組み合わせたものです。
「問題を簡単にする」は問題にする価値有るの?と思うかもしれませんが、解くことが難しい問題を解きやすくすることで、CTFに落とし込むことができます。「this is not lsb」はbleichenbacherを簡単にした問題とも考えることができますね。https://zenn.dev/kurenaif/articles/f9d3f56e1d3235 出だした「the_onetime_pad」も実はrsaのlsb oracleを簡単にした問題ですが、writeupを見る限り途中の過程も丁寧に解説されていてとても良かったなと思った記憶があります。
「天啓を待つ」は、問題そのものが降ってくるケースがあるので、それを待つケースです。SECCON2021の「oOoOoO」は大文字小文字からなんかいい感じに解けないかなぁと考えたら作れた問題です。時々こういう事があるので、思いついたら忘れないようにしないといけないですね。
「めちゃめちゃ数式を変形して面白い形にならないか試す」これはSECCON 2021の「pppp」がそうですね。「線形代数xRSA」のテーマで作問をしていて、固有値周りで色々実験してたら行列ごとできるRSA暗号を発見したので出題してみました。皆さんの驚きの声が印象に残っています。(嬉しかったですね)
問題のターゲット層を決める、誘導を作る
kurenaif的良問は、その問題を解く知識を持っていない人がコンテスト中に学習でき、学べるものです。
解ける人が瞬殺で解いてしまって、それ以降一切解かれない問題はちょっと悲しいですね。
じわじわ正解数が増えていく様子を見るのは運営の毎回の楽しみです。その点、SECCON 2022の「pqpq」は100チーム以上解けていて、それもじわじわ増えていったので目的は達成したのかなと思っています。
問題を解いてもらうためには、脆弱性のある箇所に注目させる必要があるのですが、そのためには脆弱性のある箇所以外はしっかりと安全に作り込むことが重要かなと思います。whiches symmetric examでは、「AES-GCMは正しく使われているので、AES-GCMではなく、その他のものを使って、となるとAES-OFBをつかってAES-GCMを突破できるのかな?」と思うことを期待しています。問題を解く上で、どこに気づくと解法に気づけるのかをシミュレーションしてみましょう。テスターがいるのであれば解いてもらうのが一番いいですね。
誘導が不足している場合は、コメントで補強したり、露骨に危険な実装にしたり、あえて中途半端なフィルターを実装するとそこに注目してくれると思います。
また、できることを減らすということも強力な誘導になります。例えば、リクエストをして「YesかNo」しか帰ってこないような問題は、それ以外は使えないということなので、考えることが非常に少なくなります。
SECCON 2021のcase_insensitve は問題そのものは単純ですが、誘導が少なく、solves数が少なかったのかなと思います。
動画を作る際も基本的には同じで、動画を見てくれるレベル層を設定し、最初数分はその人が分かる話を、残り20分くらいは知っていることから徐々に知らない内容にシフトさせていくようにレベルを調整しています。
(動画を作るとき)その問題に興味を持ってもらうためにはどうすればよいか?を考える。
例えば、prototype pollutionを説明するときは、そのアルゴリズムを説明するわけではなく、kibanaのRCEの画面を最初に見せ、興味を引くように工夫しました。LLLで乱数予測をする動画では、CTFの問題ではなくJavaの乱数という実際にあるものを使いました。
紹介したいアルゴリズムで検索してくる人はおそらくそのアルゴリズムを知っている人で、できれば知らない人に見てもらいたいです。
あ、これを知らないとこういう事になってしまうんだ、どうしてこうなってしまうんだろう。という興味を引く時間を最初に2,3分設けています。(実際にうまく行っているかは知りません。動画の視聴者維持率があるので、どれくらい維持できているかを指標に普段は調整しています。)
(動画を作るとき)その解説で動画特有のものを含ませることができないかを考える。
正直、ブログや書面はわかっている部分は流し読みができますし、構造も把握しやすいですし、わからなかったところは振り返りやすいですし、自分のペースで読めますし様々な利点があることはわかっています。動画よりブログのほうが良いという人が多くいることもわかっていて、自分もそう感じることは少なくないです。
ですが、文章で理解できない人が、動画という新しいアウトプットをすることで理解できるようになるかもしれません。今後の技術の発展でこういった負の側面が解消されるかもしれません。5Gになりつつある現代では、動画の視聴も気楽にできるようになりました。今後は動画のコンテンツの可能性は感じています。
こういった可能性は感じていきたいのですが、今現在負の側面があるのも事実です。負の側面を感じさせないために、できる限り普段の動画では動画特有の利点を盛り込み、動画もいけるじゃん!と思ってほしいですね。具体的には、以下のような要素を取り入れようと努力しています。
- デモと解説をシームレスに移動する
- 音、イラスト、文字をすべて利用し、複雑な情報を効率よく得る
- 今なんの話をしているのかをわかりやすくする(これはシークバーで飛ばし飛ばし見る人が、止めたいところで止めるためです。具体的には字幕を入れる、タイトルを表示するのが良いです)
- アニメーションを使う、図の変化をわかりやすくする
- 今の進捗をわかりやすくする(時間が経てばたつほど完成していく様子は楽しいですよね)
でもまだ1万再生動画はないので、まだまだ動画としては改善余地あり、ですね。
問題が正しいかを確認する
以下のことをして問題の確認をしています
- テスターがいるのであればテスターに解いてもらって問題が解けることを確認
- ランダムなフラグの値でも解けることを確認
- 問題文が与えられていて、問題を開発した環境でない環境でもとけることを確認
- 途中過程が正しいことを確認し、パラメータ等が妥当であることの確認
動画であれば、できる限りなにか主張をするのであれば似た主張をしているものを探して引用をつけるよう努力をしています。
当日は祈る
当日は非想定解放で異常に解かれてしまうことがないことを祈ります。
動画の場合は再生数が伸びることを祈ります
writeupを調べる
writeupを調べて自分の想定通りに解けてるかを確認します。このときに「楽しかった」等の意見があればとても嬉しい気持ちになります。
次
次は ゼオスTT さんより 「evilなnpmパッケージでRCE」 です。最近サプライチェーンアタックが何かとホットなので、気になるトピックですね、お楽しみにミ★
SECCON CTF 2021 の作問をさせていただきました
2019年からCTFを初めて、2021年、とうとう作問側に回ることになりました。
始めた当初はSECCONで決勝に行くことを目標にしていて、今では作問側に回る。
なんか感慨深いですね
普段一応動画の教材用に作問していますが、こういったコンテストでは初めて作問するのでドキドキでしたが、無事に終わってよかったです。
教育用の問題ばかりを作っているので難しい問題を作ることができなかった点で少し後悔しています。
次は 1solved 以上で最小の問題を作れるようになりたいですね。
作問でレビューをしてくださった皆様、先に問題を解かせてくださった皆様、インフラや運営などをしてくださった皆様、チャレンジしてくださったみなさまのおかげで無事に終了できたと思っています。本当にありがとうございました。
ここからは個別の作問の裏話をしていこうと思います。
簡易的なwriteupはこちらになるので、writeupをお求めの方はこちらを。
動画は現在鋭意作成中です。
pppp
これは Xornet さんの作った CCC があまりにもwarmupではなかったため、その場で思いついた問題をいい感じにしたものです。
RSAっぽく計算できる行列を頑張って構築しようと考えたところ、「固有ベクトルは有理数になるので、固有値も有理数だったら行けるだろ。」という思いつきを椅子に座って回転していると思いつきました。固有値を有理数にするためには上三角行列にするのが手っ取り早く、あとは複数要素同時にRSAするならGCDとか入れておけばきれいにまとまるなと思い、pを混ぜ込みました。
GCDでpを漏洩し、その後GCDでフラグを取得するという二連GCDが個人的に好きなポイントです。
予想に反してみんな直感に身を任せてd乗してくれませんでした。実際証明は思いつきにくいので、みんな式変形して解いてて偉いなぁという気持ちになりました。
oOoOoO
これは実はもともとは case insensitive のサブセットの問題でした。case insensitiveは問題の特性上大文字にしなければならなく、大文字小文字を当てるためになにかいい方法はないかと考えたところ、bytes_to_long()って実質 256^i で超増加列になるので実質ナップサック暗号じゃんという気づきを得たので作問に至りました。
bytes_to_long を mod したものは 部分和問題にならないので頭を抱えていたところ、高々文字数分総当りしたら合計値に戻せることを思いついたので、そのまま問題にしました。
ただcase insensitiveで要求される知識セットとoOoOoOで要求される知識セットがあまりにもかけ離れすぎていて、解いてて辛いだろうなと思ったので分離しました。
cerberus
なんかPadding Oracle Attackの問題作りたいなぁと思いWikipediaの図をじっと睨んでいるとivがそのまま最後のブロックに反映されて複数回同じブロックを入れると相殺することが見えたので作問しました。特に思い入れはないです
case insensitive
ßを大文字にするとSSになるという驚きの性質をしり(これに書いてました ->
O'Reilly Japan - プログラミングRust
)、その後色々調べているとffiも大文字にすると大増殖をすることをしり、bcryptかPOODLEあたりで作問しようと思っていました。ちなみに皆さんも魔力回復等に使用されるであろう Æther の Æ は小文字も大文字もあるので1文字のままです。対応している大文字や小文字がない場合特殊な処理としてこのような挙動になります。これはutf-8のしようというよりは文字そのものの仕様の側面が強いですね。
bcryptが72文字制限なのは72bytesのものとxorするフェイズがあるのですがそこでそれ以上足りなくなっちゃうからですね、これは内部で使われているblowfishの仕様です。
【日記】VTuberとして活動してきて1年ちょっとを振り返る。
この記事について
今セキュリティ・キャンプの講義資料を作っているところなのですが、親知らずを抜き、とても痛くて辛くてそれどころではないので、気を紛らわせるために書いています。 特に伝えたいなにかがあるとかそういったものではないので、気にしないでください。
どうしてVTuberとしてデビューをしたのか
おそらく競技プログラミングやCTFなどの競技性の強い趣味を持つ多くの人が同じ悩みを持っていると思うのですが、大きな理由はあらゆる趣味が「停滞したこと」だからです。 ある程度努力をすれば上位n%以上になることはできますが、順位が決定する競技でn%を維持するためには、n%以下の人より強くあり続けなければなりません。
基本的に過去の問題も蓄積されますし、私のような技術をアウトプットする魔女もいるので「自分が勉強した絶対的な量は増えているにも関わらず、相対的な順位は変わらない。」ということはしばしばあります。むしろ、学習環境が整備された後発の人のほうが勉強量は少なく同程度の水準の知識をみにつけることができるので、その歴が長い人からすると今までの苦労がいともかんたんに乗り越えられ、心が折られることもあるでしょう。
受肉以前は競技プログラミングをメインで活動してきましたが、この相対的な評価に耐えることができなくなってしまい、なにか絶対的な蓄積を得られる趣味を始めようと考えました。
そうこう悩み続けて1年ほど、VTuberというジャンルが僕たち一般人にも手に届く距離にあることがわかりました。しかしなかなか踏み出すことはできず、考えていたところVTuberの鈴原るるさんが魔界村をクリアしているのを見てなんとなくデビューを決めました。
3日ほどで絵を書きモデルを作り、とりあえず動画作成の練習に、周りからすごいと言われているVimを動画にしようと実践的Vim入門を6つ制作し、その後CTFや競技プログラミングの動画を出していきました。
教育系動画について
多くの人が言及しているように動画より書籍のほうが良いという人が多いことは把握しています。 自分もかつては同じ意見でした。
動画は書籍とは違いシークをすることはできません。 ブログ等と違って修正を加えることが困難です。 同じ内容でも圧倒的にアウトプットにコストが掛かります。
しかし動画教材はまだまだ数が少なく、踏み込む余地があると考えてアウトプットをはじめました。実際、 Zerologonの動画は論文に書いてある内容を動画で要約しただけにも関わらず、多くの反響をいただけました。同程度の内容を文字でまとめたわけではないのですが、やはり動画で伝えることのポテンシャルを感じた瞬間でした。 www.youtube.com
実際、論文だけだとわかりにくいものもカンファレンスのプレゼンテーションや先生の授業を聞くとよく分かることも多々あるので、それらをうまく組み合わせることで最高にわかりやすい教材が作れるのではないかと思っています。
さらに、昔に比べて4Gの通信環境も充実し通学時間にも動画が見れるようにもなってきました。そうした背景から今後も動画コンテンツはより気軽に見やすい世界になると思いますし、それを有効活用できる準備を今のうちに進めておいて損はないと思っています。
これまでの活動の振り返り
初期の動画のコンセプトは腐らない技術を紹介し、今後も残り続ける動画を作ることでした。 やはり初期の動画は長いことお世話になるので、できるだけ基礎的な話を心がけています。 その甲斐あってか初期の乱数の次の値を予測するなどは未だに再生数を伸ばし続けるコンテンツになっていますね 👍
動画を出しつつ、様々なフィードバックを受け、動画にも様々な変化をつけてきました。(どう変化をつけてきたかは秘密です😉 セキュリティ・キャンプのネタにするので。)わかりやすいところだと初期からフォントは変わってますね。VTuberの人気の切り抜き動画やテレビを見ながら見やすい字幕を探して編集コストが少ないものを今は採用しています。
そんなこんなで活動していると動画を視聴くださってる人間の皆さんが宣伝等していただいたおかげで、1年目に1000チャンネル登録者数を迎えることができました。正直始めた当初はマックスで1000だろうと思っていたので当時はとても驚いた記憶があります。(今ではもう1600チャンネル登録者数ですね)
とはいえ、同じ活動をしているだけでは同じ人しか視聴せず、なかなか技術が広まらないことに気づきました。また、このまま活動をし続けているとチャンネル登録者数は線形以下にしか増えず、きっとこのままつまらない成長をしてしまうのではないかと感じました。やはり1000チャンネル登録者数を達成したら次は2000ではなく10000を目指すべきです。
2年目はなにか変化をつけようとして取り組んだ活動が kurenaifChallenge であったり、魔女のお茶会であったりするわけです。1年目には知名度がなくてできなかった他人を巻き込んだ活動を2年目では実施しています。他人を巻き込むことで、より広く、より多くの人に技術を広められます。そしてチャンネル登録者数も増やせるわけです。 新しいことをするとやはりうまく行かないこともあるかとは思いますが、そっと見守ってくれると嬉しいです。次は初めて動画をプレミア公開して一緒に見てみる試みもしてみます。みんな見てくれるといいな
これからの活動について
普段の勉強用の動画の頻度は少し落ちるかもしれませんが、コミュニティ運営も少し手を出していきたいと思っています。疲弊しない程度のうまい頻度で勉強会を開催したり、CTFをやってみたり、1年目ではできなかった人を巻き込んだ活動を少しずつ進めていきたいと思います。 今でこそほとんど暗号の動画ばかりですが、様々なジャンルの深い知識がアーカイブされると嬉しいですね。それは3年目の目標です。
未来のことはよくわからないので、今掲げてる目標はこれだけです。チャンネル登録者の目標もありません。疲弊しちゃうからね
え?さっき10000を目指すって言ったじゃないかって? 確かに目指してはいますが、目標としてはおいていません。こういった活動を通じて、副次的に達成できたら嬉しいねという感じですね。
動画を上げ始めて変わったこと
やはりYouTubeにはランキングが存在しないことはとても良く、かつて相対的な評価によって疲弊することも少なくなりました。横を見渡すと自分よりチャンネル登録者数が多いセキュリティ系のYouTuberはたくさんいますが、やはり数よりも自分の前提知識の要求水準の高いレベルの動画を1600人の人が見てくれるという事実を嬉しく思います。だって1600人ですよ!?すごくないですか!?魔女のお茶会とか同時接続者数200人とかですよ!? 今ではこの数と動画の評判に心を支えてもらっています。
また、こういったアウトプットを繰り返すことで友達がたくさん増えました。自分と同水準以上に暗号を話せるととても嬉しいですし、理解も深まります。日本のいろんなCTFチームとの知り合いができからこそ、魔女のお茶会があれだけたくさんのチームに登壇していただけたのだと思っています(単純にあの手の勉強会が最近少ないのもあると思いますが)。チーム横断で知見を共有する機会を今後も増やせればいいですね。
そうして人の繋がりができた結果、セキュリティ・キャンプの講師も任せていただけるようになりましたし、まだ言えないですが他にも色々kurenaifの名前が刻まれることも増えました。以前の自分だとありえない話ですね
終わりに
そろそろ歯の痛みが収まってきたので終わりとします。まだ夕ご飯を食べてないので、これから食べます。魔女もご飯は必要です。
もし、この動画をみて自分も動画投稿を始めてみようかなと思った人は、チャンネル登録者数がほとんど増えない可能性があることを覚悟してください。僕も6ヶ月程度数十人程度のチャンネル登録者数でした。他人の考えることはよくわかりませんし、チャンネル登録者数が増えるかどうかはかなり運に依存すると思っています。他人に依存する指標を目標にしてしまうと確実に心を壊してしまうので、1000チャンネル登録者数とかを目指さずに、「前よりチャンネル登録者数が増えた」「再生時間が増えた」などといった上がりやすい指標でもって自信をつけていきましょう。学業やお仕事で忙しいのに、趣味で心を壊してしまっては意味がありませんからね。
あ、よかったらチャンネル登録もよろしくおねがいします。
それではまた、次の動画でお会いしましょう。今日の夕御飯は何にしようかな 熱いものだとまた痛みが…
競技プログラミングやCTFの動画配信/生放送でのTips
動機
最近生放送や動画配信をする人が増えてきたので、ググっただけだとわからない感覚値的なTipsを共有すると役に立つのでは?と考えて
記事にしてみた。
これから始める人は参考にしてくれると嬉しい
$whoami
僕は普段CTFの動画やwriteup生放送を中心にしている。
本格的に動き始めたのが2020年4月で、おおよそ7ヶ月目。
よかったらチャンネル登録してほしい
Youtube Livestream(生放送)編
画面上にコメントを表示するメリット
画面がうるさくなってしまったり、画面が狭くなってしまう一方、多くの配信者はそのデメリットを理解しつつコメントを画面上に表示している。
配信前まではあまりメリットに気づけなかったが、やり始めてからわかったので列挙する
実験的に表示してみた例:
コメントはしっかり読み上げてから返答する
コメントの内容は読んでから返答するべきである。
コメントを読み上げずに返答すると、どのコメントに対する返答かわからなくなってしまうため。
これは対面の会話とは違い、コメントが放送者に届くまで時間がかかるためである。
コメントは画面上に表示すると良い
利点は以下の2つ
あとで編集して再投稿したい場合、YoutubeのLivestreamではコメントが残らない。
何らかのトラブル等をカットしようにも質疑応答等のもともとのコメントが抜け落ちてしまうため、大きな損失につながる。画面上に残しておくと、後でDLすることもできるし、別の場所でも共有可能になる。
コメントをした人がタイムラグを認識することができる。
実際にコメントをしてから届くまで、そしてそれを返すまでにはそれ相応の時間がかかる。
自分のコメントが届いているのか?またいつコメントなのか?を視聴者が確認することができる。
放送者は生放送(動画)を自らダウンロードすることができる
数カ月間知らなかった BANされるリスクは誰にでもあるので、ローカルに持っておくと安心かもしれない。
フォントサイズ等の設定はスマホで見れる程度の設定にする
チャットに関しては無理なので諦めているが、自分の動画を見てくれている人の半分弱程度がiOSやAndroidからの視聴になっている(逆に言うと半分はPCから視聴している)。
おそらく競技プログラミングやCTFで似たような動画を出す人は似たような傾向になるので参考にしてほしい。
AndroidやiOSを切るということは、視聴者の半分を切るということなので、大切にするべきである。
画面上に表示するフォント等は気をつけて配信してほしい。(特に4KやWQHDなどを使っているユーザー)
どうしてもフォントサイズが変えられないようなものは、拡大鏡機能などを使用する。
キーの入力内容を表示したり、それらを反映するようなアプリは避け、動画にするべきである
生放送をしているとsudoコマンドや何らかのウェブサービスにログインする場合、パスワードなどを入力する場面が発生する可能性がある。
気をつけていてもいつかパスワードが漏洩しそうで怖いのでそのような内容は生放送では避けるべきである。
複数人でしゃべるような内容の場合、誰が喋っているか喋っているか明示するとわかりやすい
こういうツールがあるので使用しよう。誰が喋っているかわかりやすくなる。
Discordで喋ってる人を分かり易くするカスタムCSS | 萬巓堂本店
BGM使用のメリット
自分は音量調節がめんどくさくて生放送はやっていないが、動画ではBGMを使用している。
BGMを使用することで細かな雑音を気にならなくすることができる。
ノイズキャンセリングは無臭の消臭剤、こちらは香り付きの消臭剤といった感じ
ぐぐってみると意外といいフリーBGMがたくさんある。
動画編
生放送と被る部分があるので、それは排除し、動画特有の部分を列挙する
全編字幕を想定する場合、先に原稿を作っておくと効率が良い。
字幕を入れることを前提として動画を作る場合は、動画を聞く→巻き戻す→字幕を入れる→確認する。
といった編集過程が入るが、原稿があると
字幕をコピペする→適切な長さに字幕の表示時間を変更する→と、巻き戻す手間がなくなるため、非常に高速に編集を進めることができる。
これは字幕を作成する時間より圧倒的にかかるので、先に原稿を作成するメリットは大きい。
さらに原稿を先に作っておくことで、スムーズに話せるようになり、動画のテンポも上げることができる。
フィラー(「えーっと」や「うーん」)を避ける
これは動画を自分で見ていると気にするし、フィラーがないと動画編集時に音声波形が出てこなくなるので、カットして良い部分がわかりやすくなり編集効率が向上する。
沈黙はあってもカットすれば良い。恐れずに沈黙して考えてから喋ろう。
字幕フォントなどは太いものを利用し、太い縁取りを行う。(サムネイルも同様)
動画で使用するフォントは通常のフォントと違い、POPや広告に使うようなものを使うと見やすい。
また、縁取りも太く濃いものを入れておくと良い。
自分の場合は暗い色→白→暗い色と3段構造のフォントにしていて、暗い色では白い縁取りが目立ち、明るい部分では暗い縁取りがめだち、どのような背景でも目立つ色使いを心がけている。

新規参入者を獲得することが目的であれば動画は長くても15分程度
一定活動していると、長い動画でも見てくれるユーザーはいるが、これではなかなか新しいユーザーを獲得することが難しい。
今までの活動では15分以内程度の動画が人気だった。
シリーズ物は1回目以降視聴数が減少することを覚悟しよう
シリーズものも長編動画も同じで、ハードルが高くなりがちなので新規参入の障壁が高くなる。
既存ユーザーを満足させるためのコンテンツであればよいが、2回目以降は基本的にガッツリ減るのでメンタルの準備をしておこう。
動画はセクションごとに分けて撮影、編集しよう
一発取りはリスクが高いだけなので、分けれるぶんは分けておこう。
意外と動画同士の繋がりは気にならない。
時間に余裕があれば動画を見直して気になるのであればとりなおしを検討しよう
横スクロール可能なマウスやトラックパッドなどを検討しよう
動画作成時に横スクロール可能だと相当作業効率が違う。
自分はMX ERGOを使っているが、動画を作成し始めてから大きく真価を発揮した
まとめ
以上、今思いついたことを連ねてみました!
もし参考になれば幸いです
僕のアナリティクスから得られる知見もまだ隠し持っているのですが、ちょっと公開するのは恥ずかしいのでもし動画作っている人で興味があれば声をかけてくださいw
ではな ばいば~い
TSG CTF 2020 write up
TSGCTF 2020 writeup

# Beginner's Crypto
2<<10000 と 10^120のあまりがあたえられるのと同値なので、中国剰余定理を使う
# print(chineseRem(2,3,3,5)) N = len('1002773875431658367671665822006771085816631054109509173556585546508965236428620487083647585179992085437922318783218149808537210712780660412301729655917441546549321914516504576') num = 1002773875431658367671665822006771085816631054109509173556585546508965236428620487083647585179992085437922318783218149808537210712780660412301729655917441546549321914516504576 # print(chineseRem(num, 10**N, 0, 2**10000)[1]) from Crypto.Util.number import * print(long_to_bytes(chineseRem(num, 10**N, 0, 2**10000)[0] // 2**10000)) # 2**10000
# Beginner's misc
https://youtu.be/V-snPSCGyvQ?t=891
めちゃめちゃ頑張って分数を合わせる
import math # 0x777f: 552/ # 0x777e: 552+ # 0x7774: 5520 cnt = 0 out = "" i = 0 num = 552/5520 tar = -1 for i in range(5000): temp_num = 0 if tar == -1: temp = "462/" out_temp = chr(0x3b7f) for _ in range(cnt): temp += "462/" out_temp += chr(0x3b7f) temp += "462" out_temp += chr(0x3b7e) temp_num = eval(temp) print(num+temp_num) print(math.pi) if num + temp_num == math.pi: break if num+temp_num <= math.pi: out += out_temp num += temp_num else: tar = -1 cnt += 1 print(i, ':', math.pi-num) f = False for i in range(50): temp = 442/476347634763476347 if num + temp <= math.pi: if f: out += chr(0x3fbf) + chr(0x3f75) + chr(0x3f75) + chr(0x3f75) + chr(0x3f75) + chr(0x3f75) + chr(0x3f75) + chr(0x3f75) + chr(0x3f7e) f = True num += temp out += chr(0x337f) + chr(0x3fb7) + chr(0x3fb7) + chr(0x3fb7) + chr(0x3fb7) + chr(0x3ff5) else: break print(math.pi) print(num) num+=1666/6666666666666666666 out += chr(0xbbbf) + chr(0xbbba) + chr(0xbbba) + chr(0xbbba) + chr(0xbbba) + chr(0xbbbe) print(num == math.pi) with open("out.txt", "w") as f: f.write(out + chr(0x777f) + chr(0x7774) + '\n')